前言
中国有一个成语叫“鸠占鹊巢”,意思就是鸠鸟占据了鹊鸟的巢穴。布谷鸟过滤器就是基于这个成语的思想,用来解决分布式系统中的数据去重问题。
老家有一种鸟叫斑鸠,长的像鸽子, 就是一种鸠鸟;不过斑鸠会自己筑巢;
杜鹃 ,古称鸤鸠, 布谷鸟是杜鹃鸟的一种,具体来说是杜鹃科中的大杜鹃, 小时候上学, 天蒙蒙亮的时候经常听到他在树上叫唤”布谷布谷”;自己不筑巢,喜欢将蛋产在雀形目鸟类的巢中,如柳莺、大山雀、苇莺,其中,东方大苇莺是大杜鹃最喜欢寄生的鸟之一。据统计,大杜鹃能将卵寄生在 125 种其他鸟的巢中
杜鹃一般也不会在喜鹊窝里下蛋。
从体型和性格角度来看,喜鹊属于鸦科,体型比杜鹃大,且生性凶恶,杜鹃很难有机会靠近鹊巢。从实际观察记录来看,野地的实际观察中并没有杜鹃寄生在鹊巢的记录。
而红脚隼是确确实实会强占喜鹊的鸟巢来居住的
所以,“鸠占鹊巢” 从字面上理解似乎是“斑鸠/杜鹃”占了“喜鹊”的巢,但实际上在自然界中这种情况很少发生。古人可能把“雀”和“鹊”当成了同音假借字,以至于使“鸠占雀巢”,偷梁换柱成了“鸠占鹊巢”
布隆过滤器回顾
布隆过滤器有一个很明显的好处,就是我们只需要进行 n 次运算就能判断出元素是否存在于布隆过滤器中
布隆过滤器也有两个明显的缺点:
第一个缺点就是布隆过滤器的误判,由于可能存在哈希碰撞的问题,不同的元素通过哈希函数计算之后得到了相同的哈希值,进而可能会出现 “元素本来不存在于布隆过滤器,但布隆过滤器却判断其存在” 的情况,也就是我们常说的 “误判”;
第二个缺点就是BloomFilter中不允许有删除操作,因为删除后,可能会造成原来存在的元素返回不存在,这个是不允许的
布谷鸟过滤器一定程度的解决了布隆过滤器的一些问题,并且更加节省空间,是对对布隆过滤器的补充
布谷鸟哈希
最简单的布谷鸟哈希结构是一维数组结构,会有两个 hash 算法将新来的元素映射到数组的两个位置。如果两个位置中有一个位置为空,那么就可以将元素直接放进去。但是如果这两个位置都满了,它就不得不「鸠占鹊巢」,随机踢走一个,然后自己霸占了这个位置。不同于布谷鸟的是, 被踢走的元素需要找新的巢穴,但是如果这个位置也被别人占了呢?好,那么它会再来一次「鸠占鹊巢」,将受害者的角色转嫁给别人。然后这个新的受害者还会重复这个过程直到所有的“蛋”都找到了自己的“巢”为止。
而最原始的布谷鸟哈希结构采用以下步骤来解决哈希冲突:
1、对输入的Key使用两个Hash函数,得到桶中的两个位置
2、如果两个位置都为空,就把Key随机选择一个位置放入
3、如果两个位置只有一个为空,就把Key放入到这个空的位置
4、如果两个位置都不为空,则随机踢出一个元素,踢出的元素再重新计算哈希找到相应的位置
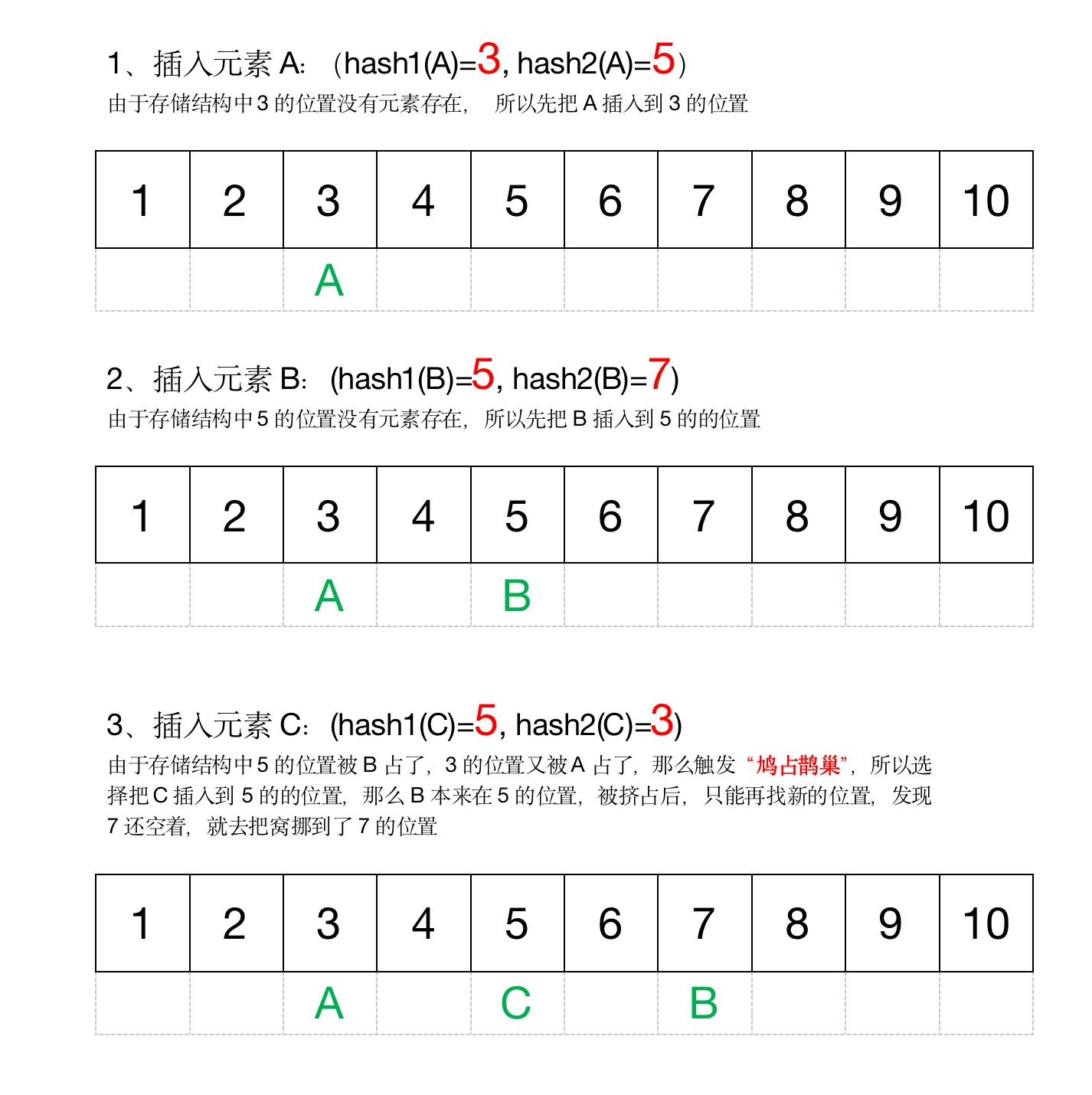
过程实例
数据插入
挤占循环
这个时候我们再插入元素D:(hash1(D)=7, hash2(D)=5)
那么D发现,7和5的位置都被占了, 就在此开始启动“鸠占鹊巢”, 把B踢走,把7的位置占了,让B去找位置去
接下来,B发现5和7的位置都被占了,那么也启动“鸠占鹊巢”,把C踢走,把5的位置占了,让C去找位置去
然后 …..
看下图
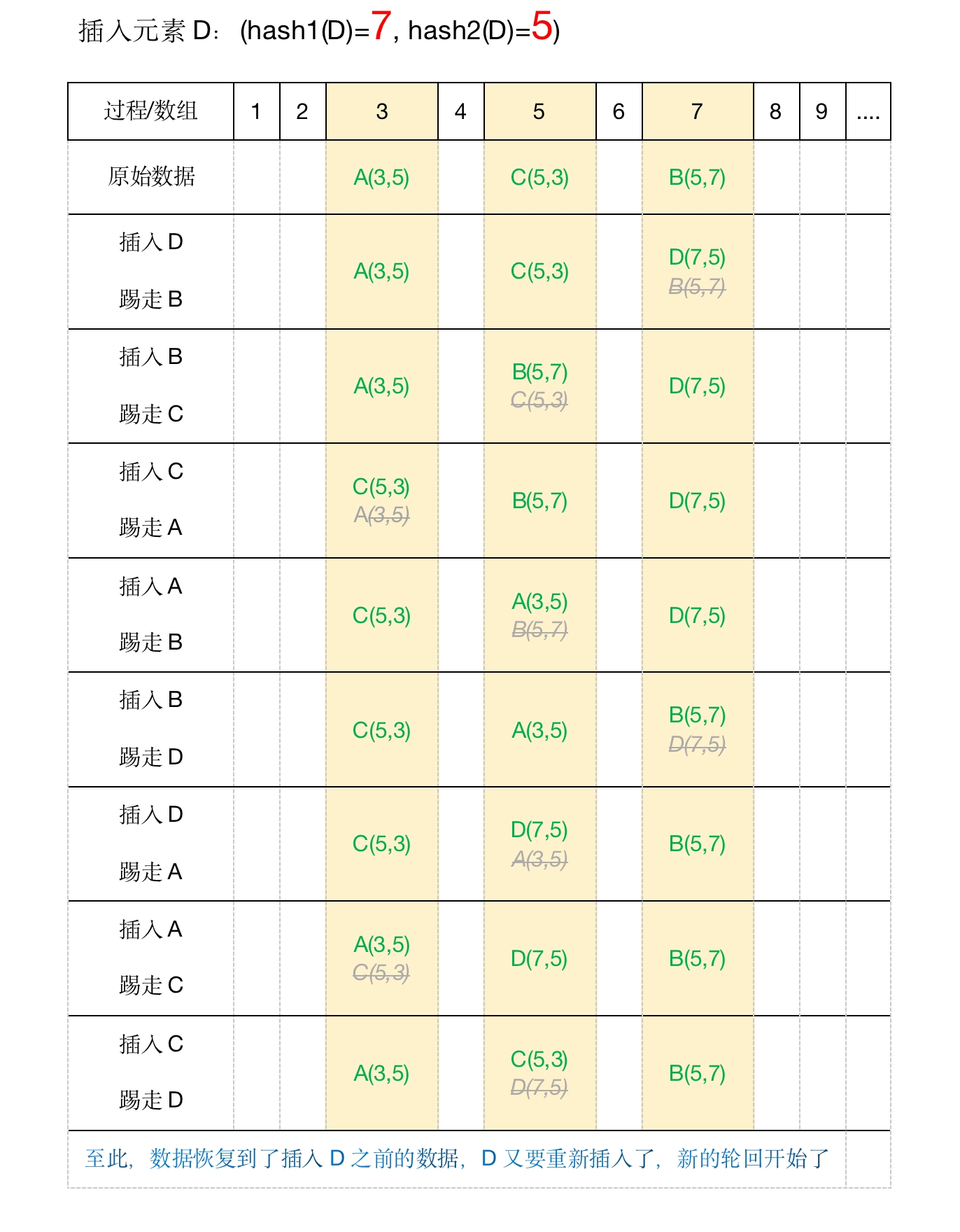
出现这种情况,就叫挤占循环
如果真的出现了4个元素,经过两次hash的情况下,依然出现了挤占循环, 那么说明你的hash算法太差劲了, 你需要考虑重新选择hash算法。
布谷鸟模型一般认为你采用的hash算法足够优秀,能够在大样本的数据量下,实现hash值的均匀分布,足够随机
由于hash算法无法100%避免hash冲突,挤占循环一定会发生; 那么可以通过增加hash函数的个数,让每个元素不止有两个巢做候选,而是三个巢、四个巢可以选择。这样可以大大降低挤占循环的概率,将空间利用率提高到 95%左右。挤占循环的概率和hash函数的个数有关, 如果你有n个hash函数,那么挤占循环的概率是(1/n)的n次方, 这个概率会随着n的增加而指数级的下降,
虽然,你有足够优秀的hash算法,并且也使用了多个hash函数, 随着数据量的增加,hash冲突会越来越多,挤占循环的概率依然会增加;
这时,我们通常会设置一个kickout次数的阈值,如果插入时出现了大量的kickout,即便不发生死循环,循环次数多了, 也会影响插入的效率,这会就要考虑扩容了
扩容
方案是在数组的每个位置上挂上多个座位,这样即使两个元素被 hash 在了同一个位置,也不必立即「鸠占鹊巢」,因为这里有多个座位,你可以随意坐一个。除非这多个座位都被占了,才需要进行挤兑。很明显这也会显著降低挤兑次数。这种方案的空间利用率只有 85%左右,但是查询效率会很高,同一个位置上的多个座位在内存空间上是连续的,可以有效利用 CPU 高速缓存。
扩容后的过程:

更加高效的方案是将上面的两个改良方案融合起来,比如使用 4 个 hash 函数,每个位置上放 2 个座位。这样既可以得到时间效率,又可以得到空间效率。这样的组合甚至可以将空间利用率提到高 98%,这是非常了不起的空间效率
指纹存储
布谷鸟过滤器中存储的是元素的指纹
指纹指的是使用一个哈希函数生成的n位比特位,n的具体大小由所能接受的误判率来设置
也就是说,我们把指纹存储到对应元素的进行哈希后所映射出来的坐标位置就好了
因为我们是对元素进行哈希计算得到指纹的,且这个指纹只有几个bit位,那么必然会导致指纹相同的情况,也就出现的误判
位置计算的对偶性
布谷鸟过滤器并没有采用先hash再对数组长度取模的方式来确定位置:
布谷鸟哈希:
fp = fingerprint(x)
p1 = hash1(x) % l
p2 = hash2(x) % l
布谷鸟过滤器:
fp = fingerprint(x)
p1 = hash1(x)
p2 = p1 ^ hash2(fp) // 异或
对偶性设计:在使用多个哈希函数时,需要设计一种机制来确保位置之间的对偶性。对偶性是指通过一个位置和存储的指纹信息可以计算出另一个位置。这种设计可以简化查找和插入操作;
实现方法:可以通过类似于布谷鸟过滤器中的异或运算来实现对偶性。例如,可以使用以下公式:
fp = fingerprint(x)
p1 = hash1(x)
p2 = p1 ^ hash2(fp)
p3 = p2 ^ hash3(fp)
p4 = p3 ^ hash4(fp)
这样,通过已知的 p1 和 x 的指纹信息,可以依次计算出 p2, p3 和 p4
上面算法中的异或运算确保了一个重要的性质:位置p2可以通过位置p1和p1中存储的指纹计算出来,就是说因为有了异或,两个位置具有对偶性。也就确保不会自己踢自己的情况
布谷鸟过滤器强制我们的数组长度为2的幂次,因为只有这样我们做异或运算的时候才可以保证计算出来的下标一定落在数组中。
数据查找
查找非常简单,在两个hash位置的桶里找一找有没有自己的指纹就 ok 了。
删除数据
也很简单,跟查找一样,在两个桶里把自己的指纹抹去就 ok 了。
重复插入问题
如果布谷鸟过滤器对同一个元素进行多次连续的插入会怎样?
如果使用了两个hash函数,根据逻辑,毫无疑问,这个元素的指纹会霸占两个位置上的所有座位,值都是一样的,都是这个元素的指纹。如果继续插入,则会立即出现挤兑循环。从 p1 槽挤向 p2 槽,又从 p2 槽挤向 p1 槽。
那么能不能在插入之前做一次检查,询问一下过滤器中是否已经存在这个元素了?这样确实可以解决问题,插入同样的元素也不会出现挤兑循环了。但是删除的时候会出现高概率的误删
如果两个元素的 hash 位置相同,指纹相同,那么这个插入检查会认为它们是相等的。
插入 x,检查时会认为包含 y。因为这个检查机制会导致只会存储一份指纹(x 的指纹)。那么删除 y 也等价于删除 x。这就会导致较高的误判率。
在现实世界的应用中,确保一个元素不被插入指定的次数那几乎是不可能做到的;
如果维护一个外部的字典来记录每个元素的插入次数呢?这个外部字典的存储空间怎么办, 说好的节约空间呢?
如果每个位置都有4个座位,反复插入同一个元素,两个位置的 8 个座位 都存储了同一个元素,那么空间浪费也是很严重的,空间效率直接被砍得只剩下 1/8,这样的空间效率根本无法与布隆过滤器抗衡了。
因为不能完美的支持删除操作,所以也就无法较为准确地估计内部的元素数量。
如果不支持删除操作,那么布谷鸟过滤器单纯从空间效率上来说还是有一定的可比性的。这确实比布隆过滤器做的要好一点,但是布谷鸟过滤器这必须的 2 的指数的空间需求又再次让空间效率打了个折扣
与布隆过滤器的比较
| 特性 | 布谷鸟过滤器 | 布隆过滤器 |
|---|---|---|
| 原理 | 基于布谷鸟哈希算法,存储元素的指纹信息,支持动态添加和删除元素 | 基于位数组和多个哈希函数,存储元素的哈希值,不支持删除操作 |
| 数据结构 | 桶数组,每个桶存储多个指纹信息 | 位数组,存储哈希值对应的位 |
| 插入操作 | 使用两个哈希函数计算两个位置,尝试插入指纹信息,如果冲突则进行“踢出”操作 | 使用多个哈希函数计算多个位置,将对应位设置为1 |
| 查询操作 | 检查两个哈希位置对应的桶中是否存在元素的指纹信息 | 检查多个哈希位置对应的位是否都为1 |
| 删除操作 | 支持删除元素,通过删除指纹信息实现 | 不支持删除操作,删除会影响其他元素的判断 |
| 空间效率 | 通常比布隆过滤器更高效,尤其是在误判率较低的情况下 | 空间效率较高,但不如布谷鸟过滤器 |
| 误判率 | 受指纹大小和桶大小影响,可以通过调整参数来控制 | 可以通过调整位数组大小和哈希函数数量来控制 |
| 适用场景 | 需要支持删除操作且对误判率有严格要求的场景 | 适用于简单的存在性检查,不需要删除操作的场景 |
布谷鸟过滤器在一定场景下相对布隆过滤器有一定优势, 但依然有自己的问题,并不能取代布隆过滤器,只能说是布隆过滤器的一种补充
java 实现
deepseek 提供的代码
import java.util.Random;
/**
* 布谷鸟过滤器实现
*/
public class CuckooFilter {
private static final int DEFAULT_CAPACITY = 1000000;
private static final int BUCKET_SIZE = 4;
private static final int MAX_KICKS = 500;
private static final int FINGERPRINT_BITS = 8;
private final byte[][] buckets;
private final int capacity;
private final Random random = new Random();
/**
* 使用默认容量构造过滤器
*/
public CuckooFilter() {
this(DEFAULT_CAPACITY);
}
/**
* 指定初始容量构造过滤器
* @param capacity 过滤器容量
*/
public CuckooFilter(int capacity) {
this.capacity = capacity;
this.buckets = new byte[capacity][BUCKET_SIZE];
}
/**
* 计算元素的指纹
*/
private byte fingerprint(byte[] data) {
// 使用简单哈希算法生成指纹(实际应使用更好的哈希函数)
int hash = 0;
for (byte b : data) {
hash = (hash * 31) + b;
}
return (byte) (hash & ((1 << FINGERPRINT_BITS) - 1));
}
/**
* 获取两个候选桶位置
*/
private int[] getBuckets(byte[] data) {
int h1 = Math.abs(data.hashCode()) % capacity;
int h2 = (h1 ^ (fingerprint(data) & 0xFF)) % capacity;
return new int[]{h1, h2};
}
/**
* 插入元素
* @return true表示插入成功,false表示插入失败
*/
public boolean insert(byte[] data) {
byte f = fingerprint(data);
int[] indexes = getBuckets(data);
// 尝试插入第一个候选桶
if (insertToBucket(indexes[0], f)) {
return true;
}
// 尝试插入第二个候选桶
if (insertToBucket(indexes[1], f)) {
return true;
}
// 需要执行踢出操作
int index = random.nextBoolean() ? indexes[0] : indexes[1];
for (int i = 0; i < MAX_KICKS; i++) {
int pos = random.nextInt(BUCKET_SIZE);
byte oldFingerprint = buckets[index][pos];
buckets[index][pos] = f;
f = oldFingerprint;
// 计算新位置
index = (index ^ (f & 0xFF)) % capacity;
if (insertToBucket(index, f)) {
return true;
}
}
return false;
}
private boolean insertToBucket(int index, byte f) {
for (int i = 0; i < BUCKET_SIZE; i++) {
if (buckets[index][i] == 0) {
buckets[index][i] = f;
return true;
}
}
return false;
}
/**
* 检查元素是否存在
*/
public boolean contains(byte[] data) {
byte f = fingerprint(data);
int[] indexes = getBuckets(data);
return checkBucket(indexes[0], f) || checkBucket(indexes[1], f);
}
private boolean checkBucket(int index, byte f) {
for (int i = 0; i < BUCKET_SIZE; i++) {
if (buckets[index][i] == f) {
return true;
}
}
return false;
}
/**
* 删除元素
*/
public boolean delete(byte[] data) {
byte f = fingerprint(data);
int[] indexes = getBuckets(data);
return removeFromBucket(indexes[0], f) || removeFromBucket(indexes[1], f);
}
private boolean removeFromBucket(int index, byte f) {
for (int i = 0; i < BUCKET_SIZE; i++) {
if (buckets[index][i] == f) {
buckets[index][i] = 0;
return true;
}
}
return false;
}
public static void main(String[] args) {
CuckooFilter filter = new CuckooFilter(1000);
byte[] data1 = "test1".getBytes();
byte[] data2 = "test2".getBytes();
filter.insert(data1);
System.out.println("Contains test1: " + filter.contains(data1));
System.out.println("Contains test2: " + filter.contains(data2));
filter.delete(data1);
System.out.println("After delete, contains test1: " + filter.contains(data1));
}
}
