视频演示:https://vd3.bdstatic.com/mda-jmi5q45r35qnvw0w/sc/mda-jmi5q45r35qnvw0w.mp4
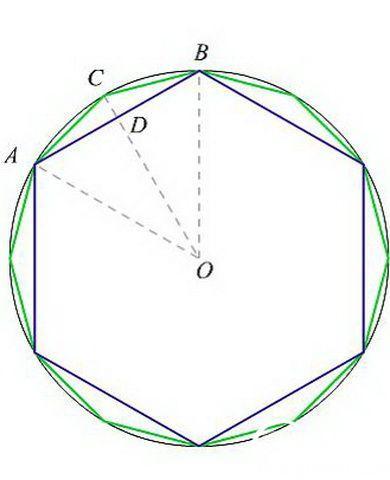
先在园内构建一个内接正六边形,那么该六边形的边长为圆的半径R;
以此为基础构建出一个内接正12变边型,根据勾股定理可以算出正12边型的边长;
继续构建出一个正24边型, 计算出边长
以此类推….
最终得到一个正N变形 为一个近似圆, 算出的边长L 乘以N 得到的正多边形的周长, 就认为是一个近似圆的周长, 除以2R就是𝛑
java 实现
public class Yuan {
public static void main(String[] args) {
circular cObj = new circular();
cObj.setRadius(1);
double pi = cObj.pi(100);
System.out.println(pi); // 输出 3.1415926535897936
// 也可以通过求面积方式求pi
// double area = cObj.area(1, 1000000000);
// System.out.println(area); // 输出 3.141592659677579 精度上差了一些
}
}
class circular {
private double radius;
private double perimeter;
public void setRadius(double radius) {
this.radius = radius;
}
public double getRadius() {
return this.radius;
}
public double getPerimeter() {
return this.perimeter;
}
public double newSide(double sideLen){
double sas = this.radius - Math.sqrt((this.radius*this.radius-sideLen*sideLen/4));
return Math.sqrt(sas*sas+sideLen*sideLen/4);
}
public double pi(int m){
double n = 6;
double sideLen = 0;
double r = this.radius;
this.perimeter = 2*this.radius;
for (int i=1; i<=m; i++) {
sideLen = this.newSide(r);
r = sideLen;
n *=2;
}
this.perimeter=sideLen*n;
return this.perimeter/(2*this.radius);
}
public double area(double r, int cutNum){
double area =0;
double y=r;
double unitLen = r/cutNum;
double x=unitLen;
while(y>0){
if((x*x+y*y)<r*r){
area+=unitLen*y;
x+=unitLen;
}else{
y-=unitLen;
}
}
return area*4;
}
}
圆周率
可以挑战下算法, 看能精确到第几位
圆周率后1000位:
PI=3.1415926535 8979323846 2643383279 5028841971 6939937510
5820974944 5923078164 0628620899 8628034825 3421170679
8214808651 3282306647 0938446095 5058223172 5359408128
4811174502 8410270193 8521105559 6446229489 5493038196
4428810975 6659334461 2847564823 3786783165 2712019091
4564856692 3460348610 4543266482 1339360726 0249141273
7245870066 0631558817 4881520920 9628292540 9171536436
7892590360 0113305305 4882046652 1384146951 9415116094
3305727036 5759591953 0921861173 8193261179 3105118548
0744623799 6274956735 1885752724 8912279381 8301194912
9833673362 4406566430 8602139494 6395224737 1907021798
6094370277 0539217176 2931767523 8467481846 7669405132
0005681271 4526356082 7785771342 7577896091 7363717872
1468440901 2249534301 4654958537 1050792279 6892589235
4201995611 2129021960 8640344181 5981362977 4771309960
5187072113 4999999837 2978049951 0597317328 1609631859
5024459455 3469083026 4252230825 3344685035 2619311881
7101000313 7838752886 5875332083 8142061717 7669147303
5982534904 2875546873 1159562863 8823537875 9375195778
1857780532 1712268066 1300192787 6611195909 2164201989
延展阅读:圆周率简史
