蒙特卡罗算法-yuyu888 Blog

蒙特卡罗算法 Monte Carlo

蒙特卡罗算法源于美国在第二次世界大战中研制原子弹的“曼哈顿计划”。该计划的主持人之一数学家冯·诺伊曼用驰名世界的赌城—摩纳哥的蒙特卡罗（Monte Carlo）来命名这种方法，其基本思想源于1777年法国数学家蒲丰提出著名的蒲丰投针实验，并以该方法求圆周率𝛑

蒙特卡罗算法的特点是，可以在随机采样上计算得到近似结果，随着采样的增多，得到的结果是正确结果的概率逐渐加大，但在（放弃随机采样，而采用类似全采样这样的确定性方法）获得真正的结果之前，无法知道目前得到的结果是不是真正的结果。

蒙特卡罗方法的步骤

蒙特卡罗方法的三个主要步骤：

描述或构造概率过程：对于已有的随机性质问题可描述和模拟这个概率过程，对于不具有随机性质的确定性问题，需要人为地构造一个概率过程。
利用概率分布抽样：通过计算机产生已知概率分布的随机变量，常用的概率分布有均匀分布，正态分布、指数分布、泊松分布等。
建立各种估计量：构造了随机概率模型，并从中抽样后，就要确定一个随机变量，作为所要求问题的解。一般是把次随机抽样结果的算术平均值作为解的近似值。

其中产生已知概率分布的随机变量是蒙特卡罗方法的重点步骤，当不知道随机变量的概率模型服从那个分布时，可以使用均匀分布来构造；
各种测量的误差、射击命中率、人的身高与体重等服从正态分布；
指数分布可用在排队论与可靠性分析中；泊松分布可用在产品检验、排队系统、物理等领域中。

拉斯维加斯算法 Las Vegas

拉斯维加斯算法又一个以赌城（Las Vegas）命名的算法，介绍的时候，一般都会与蒙特卡罗算法结对出现，方便理解

拉斯维加斯算法的特点是，随着采样次数的增多，得到的正确结果的概率逐渐加大，如果随机采样过程中已经找到了正确结果，该方法可以判别并报告，但在但在放弃随机采样，而采用类似全采样这样的确定性方法之前，不保证能找到任何结果（包括近似结果）

蒙特卡罗算法 VS 拉斯维加斯算法

场景举例

假如筐里有100个苹果，让我每次闭眼拿1个，挑出最大的。于是我随机拿1个，再随机拿1个跟它比，留下大的，再随机拿1个……我每拿一次，留下的苹果都至少不比上次的小。拿的次数越多，挑出的苹果就越大，但我除非拿100次，否则无法肯定挑出了最大的。这个挑苹果的算法，就属于蒙特卡罗算法——尽量找好的，但不保证是最好的。

而拉斯维加斯算法，则是另一种情况。假如有一把锁，给我100把钥匙，只有1把是对的。于是我每次随机拿1把钥匙去试，打不开就再换1把。我试的次数越多，打开（最优解）的机会就越大，但在打开之前，那些错的钥匙都是没有用的。这个试钥匙的算法，就是拉斯维加斯的——尽量找最好的，但不保证能找到。

结论

蒙特卡罗算法：采样越多，越近似最优解；

拉斯维加斯算法：采样越多，越有机会找到最优解；

这两类随机算法之间的选择，往往受到问题的局限。如果问题要求在有限采样内，必须给出一个解，但不要求是最优解，那就要用蒙特卡罗算法。反之，如果问题要求必须给出最优解，但对采样没有限制，那就要用拉斯维加斯算法。

蒙特卡罗算法求𝛑

提到蒙特卡罗算法，就不能提到用蒙特卡罗算法求𝛑 这个应用实例

原理

一个正方形内部相切一个圆，圆和正方形的面积之比是π/4。

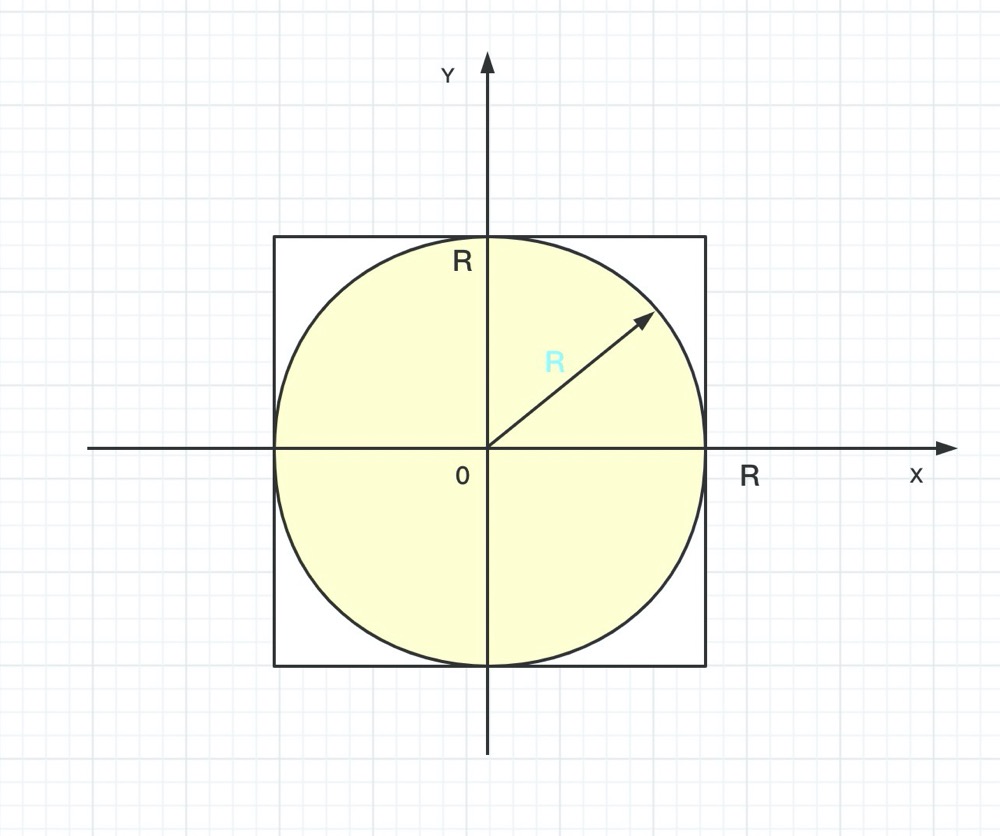
方法：在这个正方形内部，随机产生n个点（这些点服从均匀分布），计算它们与中心点的距离是否大于圆的半径，以此判断是否落在圆的内部。统计圆内的点数，与n的比值乘以4，就是π的值。理论上，n越大，计算的π值越准。

算法实现

当num 设置为 100 000 000 时，稳定返回3.14；num设置越大，可以获取的𝛑 越精确

go 实现

func MonteCarloPi(num int) float64 {
	r := 10000
	m := 0
	rand.Seed(time.Now().UnixNano())
	for i := 0; i <= num; i++ {
		x := rand.Intn(r)
		y := rand.Intn(r)
		if (x*x + y*y) <= r*r {
			m++
		}
	}
	pi := float64(4*m) / float64(num)
	fmt.Println(pi)
	pi = math.Trunc(pi*1e2) * 1e-2 //取小数点后两位
	return pi
}

蒙特卡罗算法建模

蒙特卡罗算法其实是一种思想方法，可以用于处理日常生活中的各类问题；

AlphaGo“自学成才”的关键就是蒙特卡洛算法，当然AlphaGo也不只是一个仅仅只有蒙特卡洛算法，更确切说他是蒙特卡洛算法的升级版，AlphaGo通过蒙特卡洛树搜索算法和两个深度神经网络合作来完成下棋

早餐包子问题

我一般都会去食堂吃早餐，主要吃包子但是有时候我会请假，有时候呢，又爱睡个懒觉，去晚了就不吃了，还有的时候不想吃包子，改喝粥了；
实际上在我们公司这样的人很多，所以当我去的比较晚的时候经常会发现，当我去拿包子的时候，有时候就卖没了；有时候还剩很多，肯定卖不完；
那么我就在想，食堂每天做多少个包子，能赚取最高利润（做的数量少了会导致想吃的人买不到，少卖；做的多卖不完又浪费）

假设：
1、每个包子成本价1元，售出价1.5元，根据经验过去每天最少卖1000个包子，最多卖1200个包子
2、老板的策略是每天只做固定数量的包子

使用蒙特卡罗算法，我们可以遍历1000<=n<=1200所有的n；每天做n个包子，总共做了m=10000天，来计算利润，比较利润，当利润最大时，n就是最优解

// costPrice 成本价 单位：分
// price 售卖价 单位：分
// min 最小售卖数
// max 最大售卖数
// randCount 模拟次数 该值越大越准确
func Baozi(costPrice int, price int, min int, max int, randCount int) int {
	rand.Seed(time.Now().UnixNano())
	profits := 0
	num := 0
	surplus := max - min
	for i := 0; i <= surplus; i++ {
		profitsN := 0
		for j := 0; j <= randCount; j++ {
			personNum := rand.Intn(surplus)
			if personNum >= i {
				profitsN += i * (price - costPrice)

			} else {
				profitsN += personNum*price - costPrice*i
			}
		}
		if profits < profitsN {
			profits = profitsN
			num = i
		}
	}
	return num + min
}

经过实际演算

num := Baozi(100, 150, 1000, 1200, 10000000)
fmt.Println(num)

结果稳定在1066，1065 两个数之间摆动

蒙特卡罗算法