问题引入
希望对网站的uv做一个统计,同一个用户的反复点击进入记为 1 次,重点:网站用户量很大!!!
首先, 我们最容易想到的就是使用hashmap把uid记下来,当用户来访问的时候,如果uid不存在就记个新值,最后统计下uid的个数;这种方式最容易理解,缺点是需要较大的存储空间
那么,有没有更好点的方法呢?bitmap 是个不错的选择, 可以节约几十倍的内存开支,不过依然显的有点大
假如我们并不要求绝对精确的结果,在海量的数据面前可以容忍一定的误差,那么就可以采用 HyperLogLog 算法来解决上面的计数类似问题
HyperLogLog
HyperLogLog实际上不会存储每个元素的值,它使用的是概率算法,通过存储元素的hash值的第一个1的位置,来计算元素数量
特点如下:
- 代码实现较难。
- 能够使用极少的内存来统计巨量的数据,在 Redis 中实现的 HyperLogLog,只需要12K内存就能统计2^64个数据。
- 计数存在一定的误差,误差率整体较低。标准误差为 0.81% 。
- 误差可以被设置辅助计算因子进行降低。
伯努利试验
在了解 HyperLogLog 前, 我们先了解下 伯努利试验
伯努利试验是数学概率论中的一部分内容,它的典故来源于抛硬币
硬币拥有正反两面,一次的上抛至落下,最终出现正反面的概率都是50%。假设一直抛硬币,直到它出现正面为止,我们记录为一次完整的试验,中间可能抛了 1 次就出现了正面,也可能抛了 10 次才出现正面。无论抛了多少次,只要出现了正面,就记录为一次试验。这个试验就是伯努利试验
假设我们进行了n次伯努利试验,说明有n次我们抛中了正面;其中第一次实验我们抛了K次,第一次实验我们抛掷次数记位K_1,依次类推第n次实验抛掷次数记做K_n, 其中存在最大的抛掷次数记位 K_max;
伯努利试验可以得出有以下结论:
n 次伯努利过程的投掷次数都不大于 K_max
n 次伯努利过程,至少有一次投掷次数等于 K_max
以此为基础根据一系列推导(不是很容易理解),发现在n和 K_max 中存在估算关联:n = 2^K_max
我们来验证下,假设我们每次都投K次, 设K=3, 那我们投掷出 0 0 1这个结果的概率有多大?
==排列组合==
1 0 0
1 1 0
1 0 1
1 1 1
0 1 0
0 1 1
0 0 1 <---
0 0 0
实际概率是1/8; 那么经过n轮伯努利试验后 如果我们的 K_max=3 我们可以给出一个投掷次数的估算值n=8=2^3
次伯努利试验 演算的例子
| 第 n 次伯努利试验 | 结果 | k值 |
|---|---|---|
| 1 | 0 0 1 | 3 |
| 2 | 0 1 | 2 |
| 3 | 0 0 0 1 | 4 |
| 4 | 0 0 1 | 3 |
| 5 | 0 0 0 0 1 | 5 |
| 6 | 0 0 0 0 0 0 1 | 7 |
| … | … | … |
| … | … | … |
| n | 0 0 0 0 1 | 5 |
假如K_max=7 我们可以推算出n的估值: n=2^K_max=2^7
如上例所示,假如我们实际只抛掷了10次, 则实际值远小于我们的估值2^7; 有此我们可以看出实验次数很小的时候误差很大
估算优化
如上例所示 我们认为是进行了一轮实验, 当我们的实验次数n越大的时候估算的误差率会相对减少,但仍然不够小
那么是否可以进行多轮呢?例如进行 100 轮或者更多轮次的试验,然后再取每轮的 k_max,再取平均数,即: k_mx/100。最终再估算出 n; LogLog的估算公式:

面公式的DVLL对应的就是n,constant是修正因子,它的具体值是不定的,可以根据实际情况而分支设置。m代表的是试验的轮数。头上有一横的R就是平均数:(K_max_1 + … + K_max_m)/m。
这种通过增加试验轮次,再取k_max平均数的算法优化就是LogLog的做法。而 HyperLogLog和LogLog的区别就是,它采用的不是平均数,而是调和平均数。调和平均数比平均数的好处就是不容易受到大的数值的影响。下面举个例子:
求平均工资:
A的是1000/月,B的30000/月。采用平均数的方式就是: (1000 + 30000) / 2 = 15500
采用调和平均数的方式就是: 2/(1/1000 + 1/30000) ≈ 1935.484
明显地,调和平均数比平均数的效果是要更好的。下面是调和平均数的计算方式,∑ 是累加符号
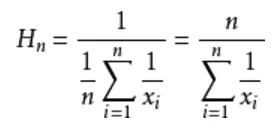
最终 HyperLogLog 的估算公式如图
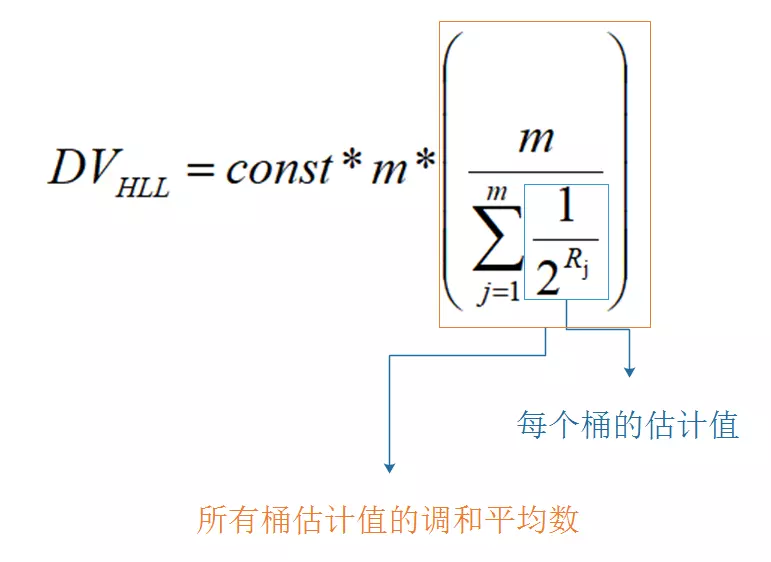
其中m是桶的数量, const 是修正常数,它的取值会根据m而变化, p是m的以2为底的对数
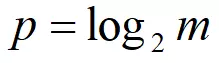
switch (p) {
case 4:
constant = 0.673 * m * m;
case 5:
constant = 0.697 * m * m;
case 6:
constant = 0.709 * m * m;
default:
constant = (0.7213 / (1 + 1.079 / m)) * m * m;
}
实战求解
回到开始的问题:
希望对网站的uv做一个统计,同一个用户的反复点击进入记为 1 次,重点:网站用户量很大!!!
如果使用 Hyperloglog 该怎么做呢?
-
对输入的数据进行hash,把数据转化为bit串
比如现在要记录三个用户的uid: 159848, 166000, 157986;由于本来就是数字,这里直接转换为二进制;
分别是:100111000001101000, 101000100001110000, 100110100100100010
实际上 Hyperloglog 是允许输入字符串的, 如果输入的是字符串,那么需要用hash算法转换成固定长度的bit串
转换成bit串后, 就可以从右往左数,记录第一次出现1的位置,记录k值,完成一次伯努利试验
-
分桶
这里把bit串的左边4位拿出来,用于分桶, 那么实际桶的数量m值为2^4 = 16; 前 4 位的二进制转为 10 进制就是桶标号。
1001 11000001101000 对应桶的编号 9
1010 00100001110000 对应桶的编号 10
1001 10100100100010 对应桶的编号 9
-
存入数据
假如通过hash算法的到的bit串位数固定; 本例中没有用hash算法 而是直接转换的二进制,所以bit串长度可能不固定;为了方便理解 假设uid大小在固定区间,二进制转换完毕后,bit位长度一致,不一致的话取可能的最大长度也行;这里假设,uid转换成bit串后,长度都是18位
那么除掉分桶的4位 还剩14位 这里可以设置桶的大小为4位, 最大 [1111] 可以最多标记15位;
实际存储的时候,先拿出前4位计算出桶编号, 然后再看后14位,记录从右往做左数第一个1出现的位置,与当前桶的值比较,如果大于当前值; 则替换
示例:
1001 11000001101000 对应桶的编号 9; K=4; K_max=4; m9=0100
1010 00100001110000 对应桶的编号 10; K=5; K_max=5; m10=0101
1001 10100100100010 对应桶的编号 9; K=2; 小于K_max,舍弃
那么最终我们存储的数据为
第1~8个桶 第9个桶 第10个桶 第11~16个桶| 0000 …. …. 0000 0100 0101 0000 …. …. 0000 -
计算
根据存储结果,套用公式反算,得出预估值
redis 怎么做的?
redis 实际是把所有输入数据hash成为64位的bit串;然后前14位最为分桶,这样实际上维护了16384个桶; 后50 用来表达伯努利过程, 每个桶的大小设位6bit 最大值 [111 1111] 可以最大表示63;可以覆盖极值 50;
所以redis 的 HyperLogLog 仅用了:16384 * 6 /8 / 1024 K = 12K 存储空间就能统计多达 2^64 个数。
Redis HyperLogLog 存储结构分为密集存储结构和稀疏存储结构两种,默认为稀疏存储结构,而我们常说的占用12K内存的则是密集存储结构。详细请参阅:深度探索 Redis HyperLogLog 内部数据结构
[参考文档]
