场景
有1亿个邮箱地址被列入了黑名单,如何判断某个邮箱地址在是否在黑名单里? 首先想到的是把邮箱地址md5一下,用HashMap存起来,判断起来十分方便,效率很高;但是每一个md5值占16字节,1亿数据就是1.6GB内存;系统开销太大
那么有没有占用内存低,效率还很高的方法呢? 前辈们早就想出了解决方案,就是大名鼎鼎的布隆过滤器。
什么是布隆过滤器
布隆过滤器(Bloom Filter)由Burton Howard Bloom在1970年提出,是一种空间效率高的概率型数据结构。它专门用来检测集合中是否存在特定的元素;它可以判断出某个元素肯定不在集合里或者可能在集合里,即它不会漏报,但可能会误报。通常应用在一些需要快速判断某个元素是否属于集合,但不严格要求100%正确的场合。
一个空的布隆过滤器是一个m位的位数组,所有位的值都为0。定义了k个不同的符合均匀随机分布的哈希函数,每个函数把集合元素映射到位数组的m位中的某一位。
优点:空间仅由二进制向量决定,并且查询时间远超一般算法(仅需计算k 个Hash函数的值);
缺点:有一定的错误识别率,并且一旦元素被添加到布隆过滤器中就很难再将该元素从布隆过滤器中删除
思想概述
网上有很多关于布隆过滤器的文章,较为晦涩的数学描述,不在此重述,这里主要通过简单的列子来阐述下他的思想,帮助初次接触者快速理解,建议先理解 bitmap原理
为了理解方便 我们把场景简化下,我需要判断某个数字是否存在已知集合
先定义存储长度位8位,定义一个简单的hash算法
function hash1($num){
return $num%8;
}
存入两个数:15,21
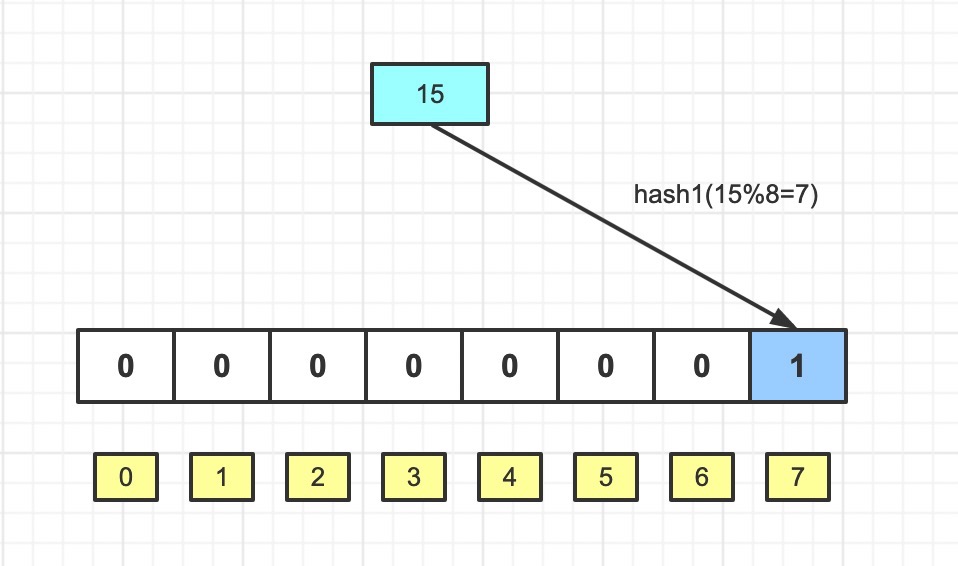
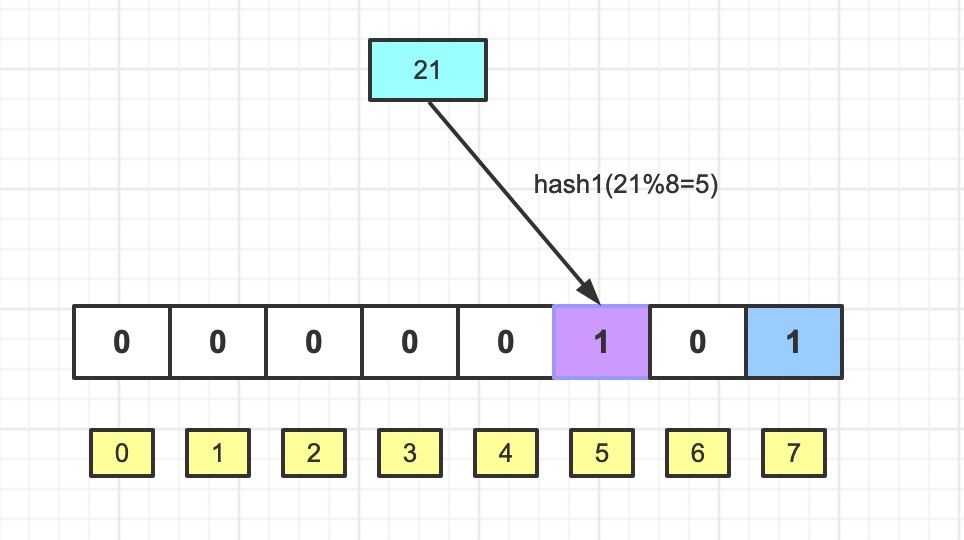
这时候我们想检查下数字11,13 是否在集合里
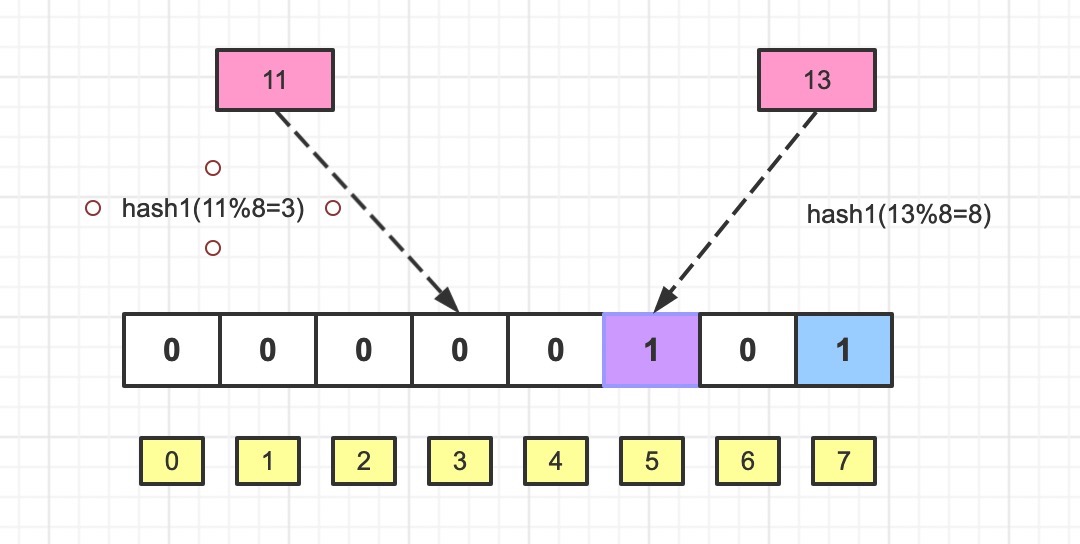
很明显11经过hash1计算后指向的位数是3,bit位的值为0; 证明该值不存在于已知集合, 那么11就一定不存在该集合了
但是13经过hash1计算后指向的位数是5,bit位的值为1; 得到的结果是13存在于已知集合,实际上是不存在的,那么这种情况就是误报
为了降低误报率, 可以使用多个hash算法,做多重校验,下面我们再新增两个hash算法
function hash2($num){
return ($num+11)%7;
}
function hash3($num){
return ($num+13)%7;
}
依旧存入15,21
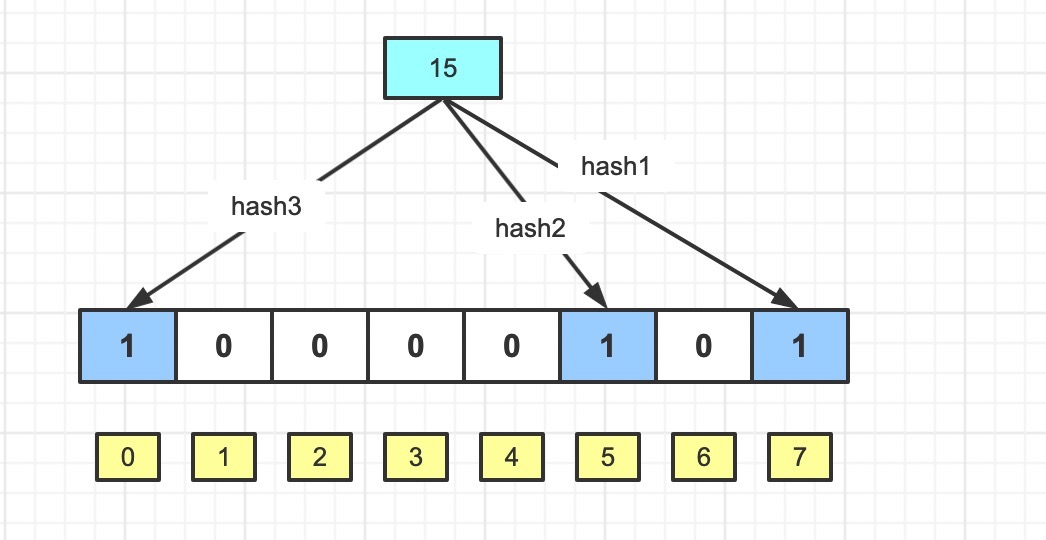
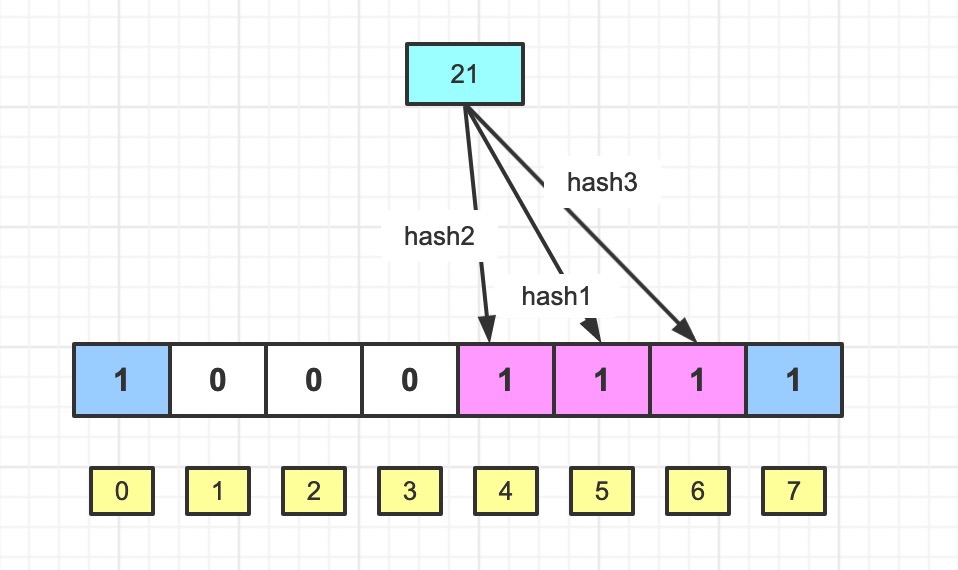
这时候我们再检查下13 是否在集合里
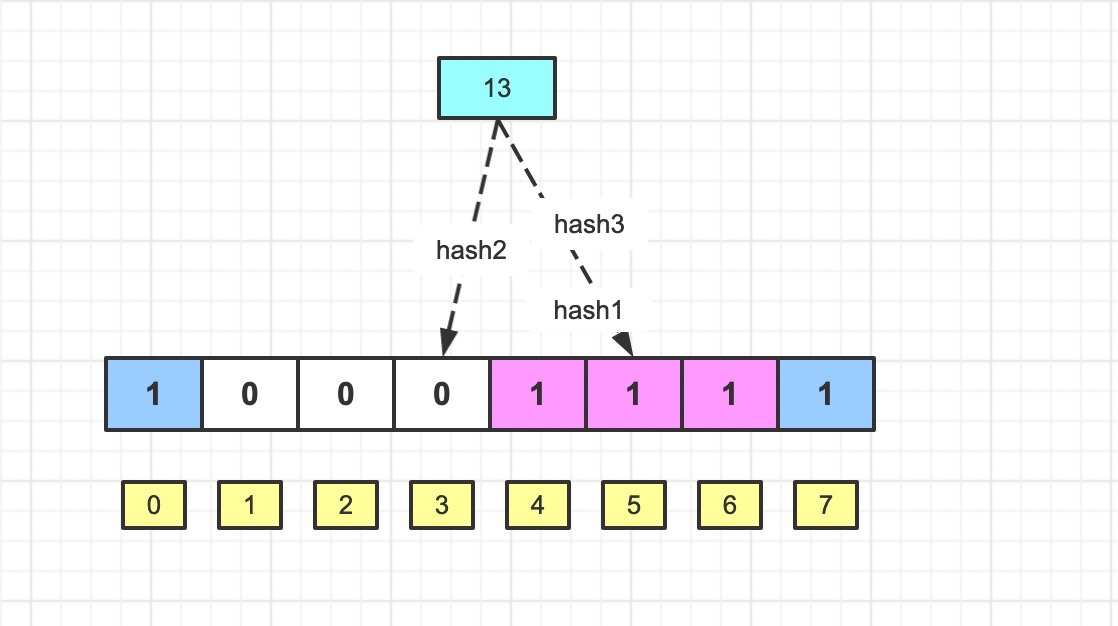
很明显,13经过三次hash的结果分别是5,3,5;其中hash1,hash3均命中结果;但是hash2的值是3, 未能命中;所以判定13不存在该集合
上述例子参数直接用的数字,随便写了几个hash函数,其实并不严谨,只是为了方便理解;实际使用上更多的是不管是数字还是字符串,统一使用hash函数变成一个数字,存放到bitmap里;如果明确纯数字的情况直接用bitmap即可
如何选择哈希函数个数和布隆过滤器长度
上例中我们设置的过滤器长度为8;实际存不了几个数,过小的布隆过滤器很快所有的 bit 位均为 1,那么查询任何值都会返回“可能存在”,起不到过滤的目的了。布隆过滤器的长度会直接影响误报率,布隆过滤器越长其误报率越小。当然布隆过滤器越长带来的存储开销也会越大
当我们把过滤器长度调的比较长的时候, 也要注意选用优秀的hash算法,尽量让数据经过hash散列后分布均匀
另外,我们发现可以增加hash函数个数,经过多次校验可以有效降低误报率;但是,哈希函数的个数也需要权衡,个数越多则布隆过滤器 bit 位置为 1 的速度越快,且布隆过滤器的效率越低
计算就不贴了, 下表是m与n比值在k个hash函数下面的误判率
k 为哈希函数个数,m 为布隆过滤器长度,n 为插入的元素个数,p 为误报率
| m/n | k | k=1 | k=2 | k=3 | k=4 | k=5 | k=6 | k=7 | k=8 |
|---|---|---|---|---|---|---|---|---|---|
| 2 | 1.39 | 0.393 | 0.400 | ||||||
| 3 | 2.08 | 0.283 | 0.237 | 0.253 | |||||
| 4 | 2.77 | 0.221 | 0.155 | 0.147 | 0.160 | ||||
| 5 | 3.46 | 0.181 | 0.109 | 0.092 | 0.092 | 0.101 | |||
| 6 | 4.16 | 0.154 | 0.0804 | 0.0609 | 0.0561 | 0.0578 | 0.0638 | ||
| 7 | 4.85 | 0.133 | 0.0618 | 0.0423 | 0.0359 | 0.0347 | 0.0364 | ||
| 8 | 5.55 | 0.118 | 0.0489 | 0.0306 | 0.024 | 0.0217 | 0.0216 | 0.0229 | |
| 9 | 6.24 | 0.105 | 0.0397 | 0.0228 | 0.0166 | 0.0141 | 0.0133 | 0.0135 | 0.0145 |
| 10 | 6.93 | 0.0952 | 0.0329 | 0.0174 | 0.0118 | 0.00943 | 0.00844 | 0.00819 | 0.00846 |
| 11 | 7.62 | 0.0869 | 0.0276 | 0.0136 | 0.00864 | 0.0065 | 0.00552 | 0.00513 | 0.00509 |
| 12 | 8.32 | 0.08 | 0.0236 | 0.0108 | 0.00646 | 0.00459 | 0.00371 | 0.00329 | 0.00314 |
| 13 | 9.01 | 0.074 | 0.0203 | 0.00875 | 0.00492 | 0.00332 | 0.00255 | 0.00217 | 0.00199 |
| 14 | 9.7 | 0.0689 | 0.0177 | 0.00718 | 0.00381 | 0.00244 | 0.00179 | 0.00146 | 0.00129 |
| 15 | 10.4 | 0.0645 | 0.0156 | 0.00596 | 0.003 | 0.00183 | 0.00128 | 0.001 | 0.000852 |
| 16 | 11.1 | 0.0606 | 0.0138 | 0.005 | 0.00239 | 0.00139 | 0.000935 | 0.000702 | 0.000574 |
| 17 | 11.8 | 0.0571 | 0.0123 | 0.00423 | 0.00193 | 0.00107 | 0.000692 | 0.000499 | 0.000394 |
| 18 | 12.5 | 0.054 | 0.0111 | 0.00362 | 0.00158 | 0.000839 | 0.000519 | 0.00036 | 0.000275 |
| 19 | 13.2 | 0.0513 | 0.00998 | 0.00312 | 0.0013 | 0.000663 | 0.000394 | 0.000264 | 0.000194 |
| 20 | 13.9 | 0.0488 | 0.00906 | 0.0027 | 0.00108 | 0.00053 | 0.000303 | 0.000196 | 0.00014 |
| 21 | 14.6 | 0.0465 | 0.00825 | 0.00236 | 0.000905 | 0.000427 | 0.000236 | 0.000147 | 0.000101 |
| 22 | 15.2 | 0.0444 | 0.00755 | 0.00207 | 0.000764 | 0.000347 | 0.000185 | 0.000112 | 7.46e-05 |
| 23 | 15.9 | 0.0425 | 0.00694 | 0.00183 | 0.000649 | 0.000285 | 0.000147 | 8.56e-05 | 5.55e-05 |
| 24 | 16.6 | 0.0408 | 0.00639 | 0.00162 | 0.000555 | 0.000235 | 0.000117 | 6.63e-05 | 4.17e-05 |
| 25 | 17.3 | 0.0392 | 0.00591 | 0.00145 | 0.000478 | 0.000196 | 9.44e-05 | 5.18e-05 | 3.16e-05 |
| 26 | 18 | 0.0377 | 0.00548 | 0.00129 | 0.000413 | 0.000164 | 7.66e-05 | 4.08e-05 | 2.42e-05 |
| 27 | 18.7 | 0.0364 | 0.0051 | 0.00116 | 0.000359 | 0.000138 | 6.26e-05 | 3.24e-05 | 1.87e-05 |
| 28 | 19.4 | 0.0351 | 0.00475 | 0.00105 | 0.000314 | 0.000117 | 5.15e-05 | 2.59e-05 | 1.46e-05 |
| 29 | 20.1 | 0.0339 | 0.00444 | 0.000949 | 0.000276 | 9.96e-05 | 4.26e-05 | 2.09e-05 | 1.14e-05 |
| 30 | 20.8 | 0.0328 | 0.00416 | 0.000862 | 0.000243 | 8.53e-05 | 3.55e-05 | 1.69e-05 | 9.01e-06 |
| 31 | 21.5 | 0.0317 | 0.0039 | 0.000785 | 0.000215 | 7.33e-05 | 2.97e-05 | 1.38e-05 | 7.16e-06 |
| 32 | 22.2 | 0.0308 | 0.00367 | 0.000717 | 0.000191 | 6.33e-05 | 2.5e-05 | 1.13e-05 | 5.73e-06 |
支持删除么
传统的布隆过滤器并不支持删除操作。但是名为 Counting Bloom filter 的变种可以用来测试元素计数个数是否绝对小于某个阈值,它支持元素删除。可以参考文章: Counting Bloom Filter 的原理和实现
php支持的各种hash函数
class BloomFilterHash
{
/**
* 由Justin Sobel编写的按位散列函数
*/
public function JSHash($string, $len = null)
{
$hash = 1315423911;
$len || $len = strlen($string);
for ($i=0; $i<$len; $i++) {
$hash ^= (($hash << 5) + ord($string[$i]) + ($hash >> 2));
}
return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF;
}
/**
* 该哈希算法基于AT&T贝尔实验室的Peter J. Weinberger的工作。
* Aho Sethi和Ulman编写的“编译器(原理,技术和工具)”一书建议使用采用此特定算法中的散列方法的散列函数。
*/
public function PJWHash($string, $len = null)
{
$bitsInUnsignedInt = 4 * 8; //(unsigned int)(sizeof(unsigned int)* 8);
$threeQuarters = ($bitsInUnsignedInt * 3) / 4;
$oneEighth = $bitsInUnsignedInt / 8;
$highBits = 0xFFFFFFFF << (int) ($bitsInUnsignedInt - $oneEighth);
$hash = 0;
$test = 0;
$len || $len = strlen($string);
for($i=0; $i<$len; $i++) {
$hash = ($hash << (int) ($oneEighth)) + ord($string[$i]); } $test = $hash & $highBits; if ($test != 0) { $hash = (($hash ^ ($test >> (int)($threeQuarters))) & (~$highBits));
}
return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF;
}
/**
* 类似于PJW Hash功能,但针对32位处理器进行了调整。它是基于UNIX的系统上的widley使用哈希函数。
*/
public function ELFHash($string, $len = null)
{
$hash = 0;
$len || $len = strlen($string);
for ($i=0; $i<$len; $i++) {
$hash = ($hash << 4) + ord($string[$i]); $x = $hash & 0xF0000000; if ($x != 0) { $hash ^= ($x >> 24);
}
$hash &= ~$x;
}
return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF;
}
/**
* 这个哈希函数来自Brian Kernighan和Dennis Ritchie的书“The C Programming Language”。
* 它是一个简单的哈希函数,使用一组奇怪的可能种子,它们都构成了31 .... 31 ... 31等模式,它似乎与DJB哈希函数非常相似。
*/
public function BKDRHash($string, $len = null)
{
$seed = 131; # 31 131 1313 13131 131313 etc..
$hash = 0;
$len || $len = strlen($string);
for ($i=0; $i<$len; $i++) {
$hash = (int) (($hash * $seed) + ord($string[$i]));
}
return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF;
}
/**
* 这是在开源SDBM项目中使用的首选算法。
* 哈希函数似乎对许多不同的数据集具有良好的总体分布。它似乎适用于数据集中元素的MSB存在高差异的情况。
*/
public function SDBMHash($string, $len = null)
{
$hash = 0;
$len || $len = strlen($string);
for ($i=0; $i<$len; $i++) {
$hash = (int) (ord($string[$i]) + ($hash << 6) + ($hash << 16) - $hash);
}
return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF;
}
/**
* 由Daniel J. Bernstein教授制作的算法,首先在usenet新闻组comp.lang.c上向世界展示。
* 它是有史以来发布的最有效的哈希函数之一。
*/
public function DJBHash($string, $len = null)
{
$hash = 5381;
$len || $len = strlen($string);
for ($i=0; $i<$len; $i++) {
$hash = (int) (($hash << 5) + $hash) + ord($string[$i]);
}
return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF;
}
/**
* Donald E. Knuth在“计算机编程艺术第3卷”中提出的算法,主题是排序和搜索第6.4章。
*/
public function DEKHash($string, $len = null)
{
$len || $len = strlen($string);
$hash = $len;
for ($i=0; $i<$len; $i++) {
$hash = (($hash << 5) ^ ($hash >> 27)) ^ ord($string[$i]);
}
return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF;
}
/**
* 参考 http://www.isthe.com/chongo/tech/comp/fnv/
*/
public function FNVHash($string, $len = null)
{
$prime = 16777619; //32位的prime 2^24 + 2^8 + 0x93 = 16777619
$hash = 2166136261; //32位的offset
$len || $len = strlen($string);
for ($i=0; $i<$len; $i++) {
$hash = (int) ($hash * $prime) % 0xFFFFFFFF;
$hash ^= ord($string[$i]);
}
return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF;
}
}
